ICDE Paper | Technical Breakthroughs of OceanBase Database in Deadlock Detection

ICDE Paper — Deadlock Detection

A paper titled “LCL: A Lock Chain Length-based Distributed Algorithm for Deadlock Detection and Resolution” was recognized at International Conference on Data Engineering (ICDE) 2023. The innovative algorithm that is proposed in this paper can accurately detect and resolve all real deadlocks in a distributed environment. The algorithm can help improve the reliability and performance of a distributed database system.

IEEE ICDE is an important international academic conference for databases. ICDE, Special Interest Group on Management of Data (SIGMOD), and the Very Large Database (VLDB) conference are the top conferences for database-related fields.

A total of 228 papers are accepted by the research track of ICDE 2023. Most papers are contributions from famous universities and scientific research institutions worldwide. OceanBase Database and Alibaba Cloud are the only companies that contributed papers to the research track of ICDE this year. Compared with the industry track, the research track module is designed to track the achievements of academic and industrial researchers and focuses more on the latest progress in data engineering. The papers that are submitted to the ICDE research track must be original and describe deep theoretical insights.

The acceptance of this paper marks that OceanBase Database provides a leading solution to distributed deadlock detection.

Comments from review experts of ICDE:

OceanBase Database proposed a lock chain length (LCL)-based deadlock detection and resolution algorithm for distributed database systems. In most cases, LCL is more suitable than other deadlock detection algorithms and can be easily configured in all types of relational database management systems (RDBMSs). In LCL-based deadlock detection, a transaction process (vertex) does not need a global wait for graph (WFG) view or a local view, but only needs to send dozens of bytes of data to the vertices that hold the resources for which the current vertex is waiting. This consumes a small amount of memory and communications resources. LCL can detect and resolve all real deadlocks in the system without inducing redundant interruptions. This paper provides a rigorous mathematical proof of the correctness of LCL and describes experiments based on a distributed transaction processing emulator (TPE) to prove the efficiency and scalability of LCL.

Abstract

Deadlock detection and resolution have been important research subject for classical relational databases for years. The distributed environment brings a new challenge for global deadlock detection and resolution. Don P. Mitchell and Michael J. Merritt (M&M) proposed a simple and fully distributed deadlock detection and resolution algorithm based on the assumption that each vertex waits for only one resource each time. As a result, this algorithm cannot be used in many usage scenarios. Inspired by the M&M algorithm, this paper presents the elegant and generally applicable LCL algorithm for resource deadlock detection and resolution in distributed environments. Extensive emulation experiments and practices in OceanBase Database prove that the LCL algorithm significantly outperforms the M&M algorithm in the efficiency of deadlock detection and resolution.

The problem of deadlock detection and resolution in database systems has been studied for decades. While it has long been a mature feature of classical centralized database systems for many years, its use in distributed database systems remains in its infancy. Don P. Mitchell and Michael J Merritt (M&M) proposed a simple and fully distributed deadlock detection and resolution algorithm, but the assumption that each process waits for only one resource each time prevents the algorithm from being used in many usage scenarios. Inspired by the M&M algorithm, we design and implement LCL, an elegant and generally applicable algorithm for resource deadlock detection and resolution in distributed environments without a restriction of the above kind. The extensive emulation experiments that are conducted by the team show that LCL significantly outperforms the state-of-the-art competitor M&M. LCL is applied to OceanBase Database, a distributed relational database system and the extensive experiments in OceanBase Database indicates that LCL is also more efficient than M&M in deadlock detection and resolution.

1. Research background

1.1 Deadlock Detection and Resolution

Deadlock detection in a distributed environment is more challenging than deadlock detection in a centralized environment. For deadlock detection in a distributed environment, each vertex has only a part of the view of the entire system and an SQL statement concurrently accesses multiple parts of a table during parallel execution. Each part may be blocked by other transaction locks. This causes each transaction to wait for multiple locks. Table 1 describes four deadlock detection and resolution algorithms.

· Centralized deadlock detection: In this algorithm, a central vertex is selected as the detector to collect information about the lock wait relationships of all vertices and generate a global WFG view. TiDB[1] applies this algorithm. This algorithm is applied only to scenarios in which lock-wait relationships are simple. The overheads of consolidating all local WFG views based on this algorithm are high.

· Deadlock prevention strategy: In this algorithm, vertices are killed based on a strategy such as Wound-Wait or Wait-Die before deadlocks occur. Google Spanner[2] applies this algorithm. Multiple transactions that do not cause deadlocks are killed. As a result, the algorithm does not meet the requirements of some users.

· Path-pushing algorithm: Each vertex builds a local WFG view and sends its local WFG view to multiple adjacent vertices. All vertices repeat this process until a vertex contains sufficient views to declare a deadlock. CockroachDB[3] applies this algorithm. Multiple vertices may detect the same deadlock and try to resolve the deadlock by killing transactions.

· Edge-chasing algorithm: In this algorithm, a special message is transmitted along the edges of the WFG of a vertex. A deadlock induces a loop and messages are returned to the initiator due to the loop. Oracle RAC and OceanBase Database[4] apply this algorithm.

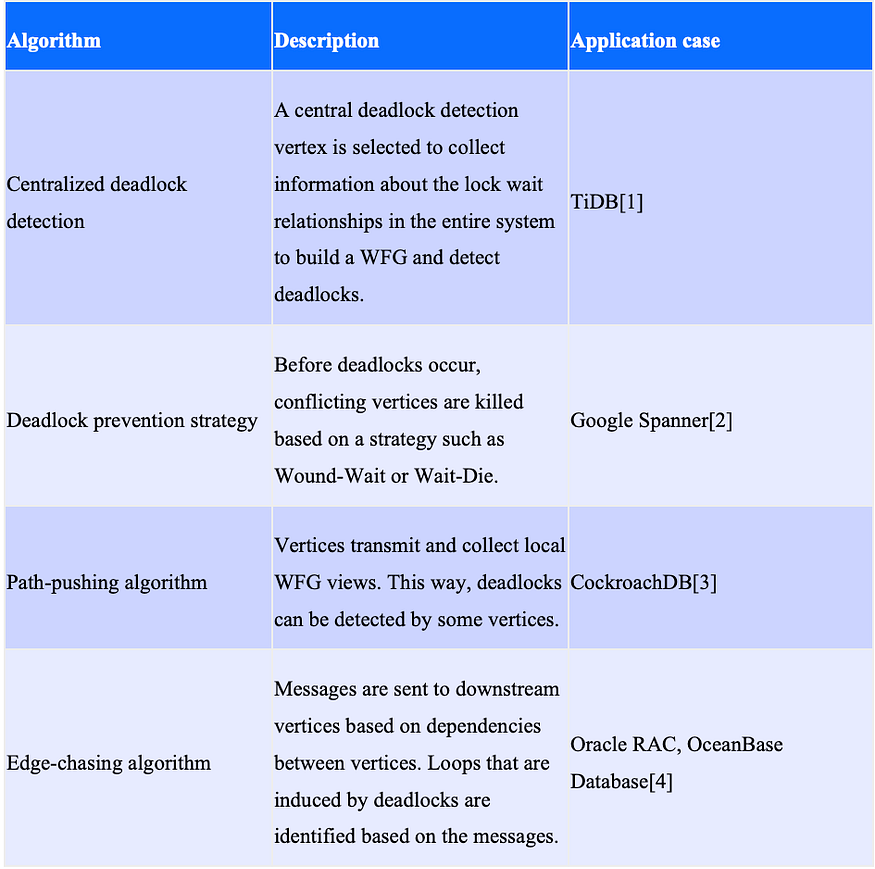
Table 1 Deadlock detection and resolution algorithms

1.2 Characteristics of deadlock detection in OceanBase Database

Each vertex does not need to build a global view or local view of vertices in the entire system but only needs to send a message to the downstream vertices for deadlock detection and resolution. Only one vertex in a deadlock loop detects and resolves deadlocks. This prevents the rollback of multiple transactions in the deadlock. Only real deadlocks are detected and resolved, and transactions that are not deadlocked are not rolled back.

2 Definitions

This article provides only the required definitions related to the LCL algorithm to facilitate understanding. This article does not provide information about the derivation process. You can obtain the entire paper from the link that is provided at the end of this article. The definition IDs in this article are consistent with the definition IDs that are specified in the paper.

2.1 Basic definitions

Definition II.1 (𝐴 → 𝐵). A → B represents an edge from vertex A to vertex B. This indicates that vertex A is waiting for some resources that are being held by vertex B. 𝐴(≠𝐵) → 𝐵 represents an edge from vertex A to vertex B and A is unequal to B.

Definition II.2 (𝐴 ⇒ 𝐵). 𝐴 ⇒ 𝐵 represents a walk from vertex A to vertex B. If 𝐴 ⇒ 𝐵 and 𝐵 ⇒ 𝐴, then 𝐴 ⇔ 𝐵.

Definition II.3 (𝐷𝑖𝑠𝑡(𝐴, 𝐵). 𝐷𝑖𝑠𝑡(𝐴, 𝐵) represents the shortest distance from vertex A to vertex B.

2.2 Annulus subgraph distance

In (𝑆𝐶𝐶(𝐴)), 𝑆𝐶𝐶(𝐴) indicates that the WFG contains the strongly connected component (SCC)[5] of vertex A.

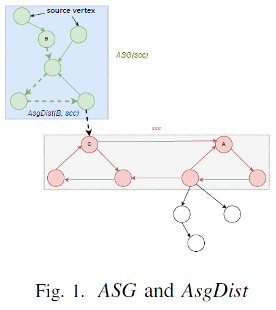
Definition II.6 (𝑈𝑆𝐺(𝑠𝑐𝑐)). 𝑈𝑆𝐺(𝑠𝑐𝑐)=(𝑉𝑆, 𝐸𝑆) represents the upstream subgraph (USG) of SCC, in which VS = {𝑋 ∈ 𝑊𝐹𝐺: 𝑋⇒𝐴, 𝐴 ∈ 𝑠𝑐𝑐}, 𝐸𝑆= {𝑋 → 𝑌: 𝑋 ∈ 𝑉𝑆 𝑎𝑛𝑑 𝑌 ∈ 𝑉𝑆 𝑎𝑛𝑑 𝑋 → 𝑌 ∈ 𝑊𝐹𝐺}.

Definition II.7 (𝐴𝑆𝐺(𝑠𝑐𝑐)). 𝐴𝑆𝐺(𝑠𝑐𝑐)=(𝑉𝑆, 𝐸𝑆) represents the annulus subgraph (ASG) of SCC, in which 𝑉𝑆={𝑋 ∈ 𝑊𝐹𝐺: 𝑋 ∈ 𝑈𝑆𝐺(𝑠𝑐𝑐) 𝑎𝑛𝑑 𝑋 ∉ 𝑠𝑐𝑐}, 𝐸𝑆={𝑋 → 𝑌: 𝑋 ∈ 𝑉𝑆 𝑎𝑛𝑑 𝑌 ∈ 𝑉𝑆 𝑎𝑛𝑑 𝑋 → 𝑌 ∈ 𝑊𝐹𝐺}.

Definition II.8 (𝐴𝑠𝑔𝐷𝑖𝑠𝑡(𝐴, 𝑠𝑐𝑐)). 𝐴𝑠𝑔𝐷𝑖𝑠𝑡(𝐴, 𝑠𝑐𝑐)=max{𝑚: 𝐸𝑥𝑖𝑠𝑡 𝑚 𝑑𝑖𝑠𝑡𝑖𝑛𝑐𝑡 𝑣𝑒𝑟𝑡𝑖𝑐𝑒𝑠 Cm(=𝐴), Cm-1, …, C1 in 𝐴𝑆𝐺(𝑠𝑐𝑐) 𝑎𝑛𝑑 𝑎 𝑣𝑒𝑟𝑡𝑖𝑐𝑒𝑠 C0 ∈ 𝑠𝑐𝑐 such that Cm(=𝐴) → Cm-1 → … → C1 → C0 } represents the distance from vertex A to SCC in the ASG of SCC.

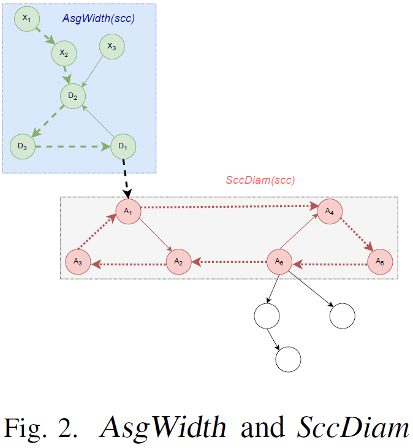
Definition Ⅲ.1 (𝐴𝑠𝑔𝑊𝑖𝑑𝑡ℎ(𝑠𝑐𝑐)). 𝐴𝑠𝑔𝑊𝑖dth(𝑠𝑐𝑐):=max{𝐴𝑠𝑔𝐷𝑖𝑠𝑡(𝑋, 𝑠𝑐𝑐): 𝑋 ∈ 𝑈𝑆𝐺(𝑠𝑐𝑐)} represents the width of the ASG of SCC.

Definition Ⅲ.8 (𝑆𝑐𝑐𝐷𝑖𝑎𝑚(𝑠𝑐𝑐)). 𝑆𝑐𝑐𝐷𝑖𝑎𝑚(𝑠𝑐𝑐):=max{𝐷𝑖𝑠𝑡(𝑋, 𝑌): 𝑋 ∈ 𝑠𝑐𝑐 𝑎𝑛𝑑 𝑌 ∈ 𝑠𝑐𝑐} represents the diameter of SCC.

2.3 Other definitions in the LCL algorithm

Definition Ⅲ.2/4 (<𝑃𝑟𝐴𝑃,𝑃𝑟𝐼𝐷>). 𝑃𝑟𝐼𝐷 and 𝑃𝑟𝐴𝑃 are the private constant ID and priority of each vertex. In a deadlock, the vertex that has the largest <𝑃𝑟𝐴𝑃,𝑃𝑟𝐼𝐷> values is killed to resolve the deadlock.

Definition III.3/5 (<𝑃𝑢𝐴𝑃,𝑃𝑢𝐼𝐷>). 𝑃𝑢𝐼𝐷 and 𝑃𝑢𝐴𝑃 are the non-constant ID and priority. Their initial values are respectively equal to the values of 𝑃𝑟𝐼𝐷 and 𝑃𝑟𝐴𝑃.

Definition Ⅲ.6 (𝐿𝐶𝐿𝑉). 𝐿𝐶𝐿𝑉 is the LCL value of the vertex whose initial values are 0. In most cases, 𝐴.𝐿𝐶𝐿𝑉=𝑚 indicates that a walk of length m from a vertex to A exists.

Definition Ⅲ.7 (max{𝑆.𝐿𝐶𝐿𝑉}). Let S be a subset of WFG, max{S.𝐿𝐶𝐿𝑉}:=max{𝑋.𝐿𝐶𝐿𝑉: 𝑋 𝑖𝑠 𝑎 𝑣𝑒𝑟𝑡𝑒𝑥 𝑖𝑛 𝑆}. The meanings of max{𝑆.<𝑃𝑢𝐴𝑃, 𝑃𝑢𝐼𝐷>} and max{𝑆.<𝑃𝑟𝐴𝑃, 𝑃𝑟𝐼𝐷>} are similar.

Definition Ⅲ.9 (LCL Proliferation). An LCL proliferation deduction on an edge A(≠B) → B is defined as: A.<PuAP, PuID>=A.<PrAP, PrID>, B.<PuAP, PuID>=B.<PrAP, PrID>, B.LCLV=max(B.LCLV, A.LCLV+1).

Definition Ⅲ.10 (LCL Spread). An LCL spread deduction on an edge A(≠B) → B is defined as: B.LCLV=max(B.LCLV, A.LCLV). If B.LCLV==A.LCLV, then B.<PuAP, PuID>=max(B.<PuAP, PuID>, A.<PuAP, PuID>).

The LCL proliferation/spread deduction is applied on each edge in WFG at least once. The exact times when the deduction is applied on each edge and the order of application are arbitrary.

3 What is the LCL algorithm

The LCL algorithm is a distributed deadlock detection algorithm that is classified as an edge-chasing algorithm. In this algorithm, LCL values indicate the dependencies on resources that are required by transactions for access. The algorithm comprises three stages: proliferation, spread, and detection.

In each stage, if vertex A triggers a detection event, A sends its LCLV, <PuAP, PuID>, and PrID to all its direct downstream vertices. After the direct downstream vertices receive the information, each direct downstream vertex of vertex A executes the corresponding LCL operation based on the stage and sends notifications to direct downstream vertices. An LCLV in ASG(scc) can spread to SCC after up to AsgWidth(scc) rounds of deduction are performed. Then, the LCLV of the vertex in ASG(scc) no longer increases. As shown in Figure 2, A1 → A2 → A3 → A1 is a cycle in SCC. If the time for proliferation is not limited, the LCLV of the vertex on the cycle can be arbitrarily large. Therefore, the LCL algorithm provides a time limit.

3.1 LCL proliferation

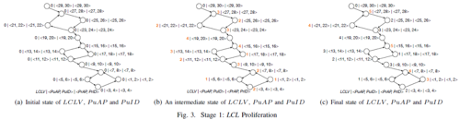
max(AsgWidth(scc), 1) rounds of LCL proliferation deduction are performed during the proliferation stage. The time complexity is (N × M1), in which N is the number of directed edges in WFG and M1 is AsgWidth(scc), which is the width of the ASG of SCC. Figure 3(a) shows the LCLV and <PuAP,PuID> of each vertex in the initial state in the proliferation stage. Figure 3(b) shows the state of each vertex during the deduction process. The order of deduction on the edges is random. Figure 3(c) shows the state of each vertex after the proliferation stage ends.

3.2 LCL spread

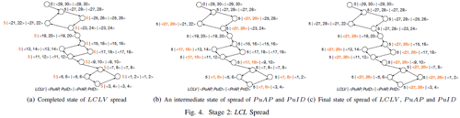
2 × 𝑆𝑐𝑐𝐷𝑖𝑎𝑚(𝑠𝑐𝑐) rounds of spread deduction are performed during the spread stage. The time complexity is 𝑂(𝑁 × M2), in which N is the number of directed edges in WFG, and M2 is 𝑆𝑐𝑐𝐷𝑖𝑎𝑚(𝑠𝑐𝑐), the diameter of SCC. Figure 4(a) shows the LCLV spread result during the spread stage. Figure 4(b) shows the intermediate states of the spread of PuAP and PuID during the stage. Figure 4(c) shows the state of each vertex after the spread stage ends.

3.3 LCL detection

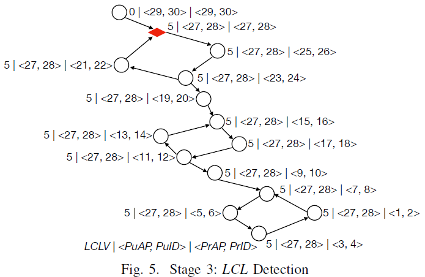
Deduction on 𝐴(≠𝐵) → 𝐵 in the LCL detection stage: If 𝐵.𝐿𝐶𝐿𝑉==𝐴.𝐿𝐶𝐿𝑉 and 𝐵.<𝑃𝑢𝐴𝑃, 𝑃𝑢𝐼𝐷>==𝐴.<𝑃𝑢𝐴𝑃, 𝑃𝑢𝐼𝐷> and 𝐵.<𝑃𝑢𝐴𝑃, 𝑃𝑢𝐼𝐷>==B.<𝑃r𝐴𝑃, 𝑃r𝐼𝐷>, B detects a deadlock and releases the resources. The time complexity in the proliferation stage is 𝑂(𝑁), in which N is the number of directed edges in WFG. Figure 5 shows a deadlock that is detected in the system.

3.4 Logic of the LCL algorithm

Definition IV.2 (proper upstream SCC). If 𝑠𝑐𝑐2⊆𝐴𝑆𝐺(𝑠𝑐𝑐1), 𝑠𝑐𝑐2 is determined to be a proper upstream SCC of scc1.

Definition IV.3 (topmost SCC). An SCC is determined to be a topmost SCC if a proper upstream SCC does not exist.

Theorem IV.5. In WFG, if an SCC exists, at least one topmost SCC exists.

In WFG, if deadlocks exist, SCCs must exist and one of them must be a topmost SCC. For more information about the derivation process, see the appendix of the paper.

Lemma IV.10. During the LCL proliferation stage, SCC is the topmost SCC in WFG. After at least w rounds of LCL proliferation deductions,

(1) the LCLV of each vertex in 𝐴𝑆𝐺(𝑠𝑐𝑐) is invariant.

(2) if ∀X ∈ ASG(scc) and ∀Y ∈ USG(scc) such that X(≠Y ) → Y, then X.LCLV < Y.LCLV; and

(3) max{𝐴𝑆𝐺(𝑠𝑐𝑐).𝐿𝐶𝐿𝑉} < max{𝑠𝑐𝑐.𝐿𝐶𝐿𝑉} = max{𝑈𝑆𝐺(𝑠𝑐𝑐).𝐿𝐶𝐿𝑉}

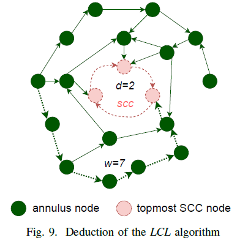
Figure 9 shows the deduction process of LCL. The vertex at the outermost circle of ASG needs up to 𝐴𝑠𝑔𝑊𝑖𝑑𝑡h(𝑠𝑐𝑐) steps to pass through other vertices to spread the LCLV to SCC. After the LCL proliferation stage, the LCLVs of vertices in 𝐴𝑠𝑔(𝑠𝑐𝑐) no longer change and are smaller than the LCLVs of the vertices in SCC on which the preceding vertices depend. In the LCL spread stage, a vertex in 𝐴𝑆𝐺(𝑠𝑐𝑐) cannot change the <𝑃𝑢𝐴𝑃,𝑃𝑢𝐼𝐷> of a vertex in SCC.

Theorem IV.11. If SCC is the topmost SCC in WFG, let 𝑤=𝐴𝑠𝑔𝑊𝑖𝑑𝑡ℎ(𝑠𝑐𝑐) and 𝑑=𝑆𝑐𝑐𝐷𝑖𝑎𝑚(𝑠𝑐𝑐). After at least max{𝑤, 1} rounds of LCL proliferation and 2 × 𝑑 rounds of LCL spread, only vertex A meets the following requirements: 𝐴(≠𝐵) → 𝐵 and 𝐵.𝐿𝐶𝐿𝑉==𝐴.𝐿𝐶𝐿𝑉 and 𝐵.<𝑃𝑢𝐴𝑃,𝑢𝐼𝐷>==𝐴.<𝑃𝑢𝐴𝑃,𝑃𝑢𝐼𝐷> and 𝐵.<𝑃𝑢𝐴𝑃,𝑃𝑢𝐼𝐷>==𝐵.<𝑃𝑟𝐴𝑃,𝑃𝑟𝐼𝐷>. B is the vertex that has the largest <𝑃𝑟𝐴𝑃,𝑃𝑟𝐼𝐷> in SCC.

In SCC, the vertex that has the largest <𝑃𝑟𝐴𝑃,𝑃𝑟𝐼𝐷> is unique and can meet the detection requirements and lock the topmost SCC. The LCL algorithm can ensure that deadlocks in the topmost SCC are detected and resolved. After deadlocks in the topmost SCC are resolved, other potential deadlocks are detected in the subsequent rounds of detection.

4 Implementation of LCL in OceanBase Database

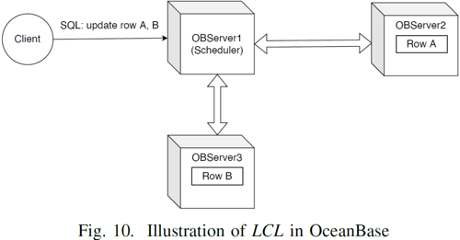
Figure 10 shows how LCL is implemented in OceanBase Database. The client connects to OBServer1 in the cluster and starts a transaction. OBServer1 is referred to as the transaction coordinator. An SQL statement that is submitted to perform data row modifications is routed to the Paxos leader for execution. A lock conflict with the leader may cause an execution failure. The transaction coordinator obtains information from the failed subtask and builds dependencies. During the LCL deduction process, a special message is transferred based on the dependencies at regular intervals to detect and resolve possible deadlocks.

5 Performance test

5.1 Comparison between the M&M and LCL algorithms

The M&M algorithm[6] is a simple and fully distributed edge-chasing algorithm that helps detect and resolve deadlocks. The LCL algorithm proposed by OceanBase Database is inspired by the M&M algorithm. The difference between the algorithms is that M&M assumes that the transaction waits for only one resource but LCL does not limit the number of resources for which the transaction can wait.

5.2 TPE

In transaction processing simulation experiments, a table that contains the same number of rows is created on each database node. The workloads are transactions that contain two types of SQL statements: (1) update operations that need to apply for lock resources. These operations comprise approximately 50% of the total number of operations; (2) query requests that do not need to apply for lock resources. These operations also comprise approximately 50% of the total number of operations. SQL statements in each transaction and resources for which the SQL statement applies are exponentially distributed or normally distributed. During the entire test process, the TPE continuously generates, executes, and commits transactions. In actual implementation, all transactions are included in a global array. The private ID is the array index. The private priority is generated by an auto-increment integer sequence on each database node. This is similar to the start timestamp of a transaction.

5.3 TPE experiment configurations

LCL algorithm configurations: Each round of LCL deduction is performed for 2,640 ms. The LCL proliferation process requires 1,200 ms, the LCL spread process requires 1,200 ms, and the LCL detection process requires 240 ms. Each emulation experiment is run for 300s, and no new transactions are generated after the experiment is completed. The generated transactions are executed until they are committed or rolled back.

5.4 TPE experiment result

When all SQL statements and resources are exponentially distributed, and each table contains 400,000 rows, the number of detected deadlocks and the number of committed transactions increase linearly over time. The LCL algorithm supports multiple out-degrees. Compared with the single-out-degree M&M algorithm, the LCL algorithm improves the efficiency of deadlock detection and ensures that fewer deadlocks exist. The LCL algorithm runs in a multi-out-degree transaction processing system that supports parallel transaction execution to ensure a higher throughput compared with M&M which runs in a single-out-degree system.

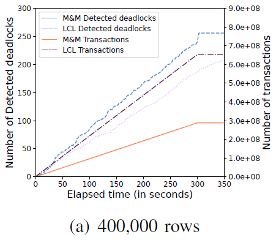
Figure 11 shows the changes in the number of detected deadlocks and the number of completed transactions in the LCL and M&M algorithms when the number of rows in each table is increased. When the number of rows increases from 400,000 to 600,000, 900,000, and 1,000,000, the number of row lock conflicts is decreased. As a result, the number of deadlocks is decreased and the number of committed transactions is increased.

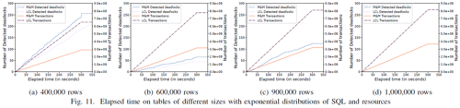
In the paper, three other experiments are also performed. In the second experiment, SQL statements are exponentially distributed and resources are normally distributed. In the third experiment, SQL statements are normally distributed and resources are exponentially distributed. In the last experiment, SQL statements and resources are normally distributed.

5.5 Experiment verification on OceanBase Database

(1) OceanBase Database cluster: In the experiment, the OceanBase Database cluster contains nine servers, and each server uses Intel(R) Xeon(R) Platinum 8269CY CPU @ 2.50GHz, 256 GB of memory, and GbE.

(2) Resources and workloads: Tables on all nodes contain the same number of rows that ranges from 2,000 to 6,000. The distribution mode of SQL statements is the same as the distribution mode in the TPE experiment.

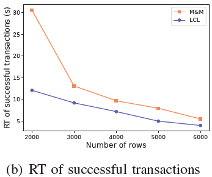
(3) Exponential distribution of SQL statements and resources: The LCL algorithm allows a transaction to apply for multiple resources at a time. After the deadlock is resolved and multiple resources are released, the transaction can be quickly executed. In the M&M algorithm, the transaction execution process is blocked on an SQL statement that applies for resources, and more deadlocks occur. The number of committed transactions in the LCL algorithm is 40% more than that in the M&M algorithm.

If no lock conflict occurs, the execution time of a single transaction must be less than 100 ms. The response time (RT) of each transaction is high due to lock conflicts. The M&M algorithm detects only one out-degree and can miss deadlocks. If a transaction times out, a high latency occurs for other waiting transactions. The LCL algorithm detects all out-degrees and resolves deadlocks in an effective manner. The algorithm outperforms M&M in latency.

6 Conclusion

According to the rigorous mathematical proof, the LCL algorithm can ensure that all deadlocks are detected and only one vertex in a deadlock cycle detects deadlocks. The experiment results show that because of multiple out-degrees, the LCL algorithm outperforms the M&M algorithm in the deadlock detection efficiency, transaction throughput, and transaction RT. The LCL algorithm can be easily implemented in a distributed relational database and used in many usage scenarios. The algorithm is widely applied in OceanBase Database. The paper is uploaded to GitHub. You can obtain the entire paper from the following webpage: https://github.com/oceanbase/LCL/blob/master/LCL_full.pdf.

References

[1] Dongxu Huang, Qi Liu, Qiu Cui, Zhuhe Fang, Xiaoyu Ma, Fei Xu, Li Shen, Liu Tang, Yuxing Zhou, Menglong Huang, et al. TiDB: a Raft-based HTAP database. Proceedings of the VLDB Endowment, 13(12):3072–3084, 2020.

[2] David F Bacon, Nathan Bales, Nico Bruno, Brian F Cooper, Adam Dickinson, Andrew Fikes, Campbell Fraser, Andrey Gubarev, Milind Joshi, Eugene Kogan, et al. Spanner: Becoming a sql system. In Proceedings of the 2017 ACM International Conference on Management of Data, pages 331–343, 2017.

[3] Rebecca Taft, Irfan Sharif, Andrei Matei, Nathan VanBenschoten, Jordan Lewis, Tobias Grieger, Kai Niemi, Andy Woods, Anne Birzin, Raphael Poss, et al. Cockroachdb: The resilient geo-distributed sql database. In Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data, pages 1493–1509, 2020.

[4] Zhenkun Yang, Chuanhui Yang, Fusheng Han, Mingqiang Zhuang, Bing Yang, Zhifeng Yang, Xiaojun Cheng, Yuzhong Zhao, Wenhui Shi, Huafeng Xi, Huang Yu, Bin Liu, Yi Pan, Boxue Yin, Junquan Chen, and Quanqing Xu. OceanBase: A 707 Million tpmC Distributed Relational Database System. Proceedings of the VLDB Endowment, 15(12):3385–3397, 2022.

[5] Robert Tarjan. Depth-first search and linear graph algorithms. SIAM journal on computing, 1(2):146–160, 1972.

[6] Don P Mitchell and Michael J Merritt. A distributed algorithm for deadlock detection and resolution. In Proceedings of the third annual ACM symposium on Principles of Distributed Computing, pages 282–284, 1984.